Задача 1
В выпуклом
четырёхугольнике ABCD
длина отрезка, соединяющего середины диагоналей, равна длине отрезка,
соединяющего середины сторон AD
и
BC.
Найдите величину (в градусах) меньшего из углов, образованных прямыми AB и
CD.

В трапеции ABCD точка М лежит на боковой стороне AB, O – точка пересечения диагонали BD и
отрезка CM.
Найти площадь треугольника COD,
если AM=MB, CO=4OM, а площадь треугольника BOM равна 1.
Решение
Задача 5
На окружности радиуса 5, описанной около правильного
треугольника АВС, взята точка М. Известно, что расстояние от точки М до одной
из вершин треугольника равно 9. Сумма расстояний от точки М до двух других
вершин равна…
Решение
Задача 7
Основание треугольника равно 20 см. Медианы боковых
сторон – 18 см и 24 см. Найдите площадь треугольника.
Решение
Вспомним утверждение о равновеликости фигур: три
медианы треугольника делят его на шесть равновеликих треугольников.

Задача 8
В
треугольнике АВС провели биссектрису AL, M - середина
стороны АС.
Оказалось,
что AL=LM. Известно, что
АВ=7, АС =18. Найдите длину стороны треугольника АВС.
Решение
В прямоугольном треугольнике АВС (∠C=90o) провели биссектрису AD; отрезок, соединяющий её основание с точкой пересечения медиан, перпендикулярен катету. Найти углы треугольника.
Задача 10
Медианы
треугольника равны 3;4 и 5. Найдите площадь треугольника.
Задача 11
В треугольнике
АВС, АВ=ВС, угол САВ равен 300 , АЕ – биссектриса треугольника, ВЕ=8
см. Найдите площадь треугольника.
Задача 12
В треугольнике АВС, АВ=12, ВС=36, cos∠ABC= -(2√2)/3, BL – биссектриса треугольника. Найдите площадь треугольника ABL.
Задача 13


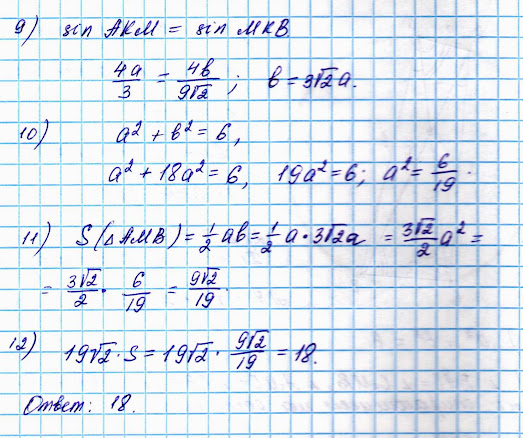




.jpg)





Комментариев нет:
Отправить комментарий